Newton’s two ‘Moon-tests’
British Journal for history of Science 1991 24 369-72
This note examines the most famous of Isaac Newton’s calculations, which compared as it were the apple and the moon in their fall, and we see how the 100% error in his lunar mass estimate impacted into it. I used when composing this the 2nd Edition of his Principia of 1713, without realizing that in the first Edition of 1685 the error was even larger (as Curtis Wilson pointed out to me) – 200%! In a sense this did not matter, because in the First Edition he made no estimate of the baricentre, i.e. he performed his Moon-test as a one-body computation, and not, as in 1713, a two-body computation. (2004)
Two somewhat different versions of the ‘Moon-test’ occur in the third edition of Newton’s Principia. This historic computation was briefly outlined in Proposition IV of Book III as a one-body computation, then Proposition XXXVII gave a more elaborate two-body computation worked out to nine-figure accuracy. In the first of these the Moon is made to orbit around the centre of the Earth, while in the second it orbits around a baricentre, the centre of gravity of the Earth-Moon system.
It has been argued by Westfall that the accuracy of the Moon-test, as given in the second of these computations, was greatly exaggerated, and that in effect Newton had worked backwards from a known and relatively accurate value for the rate of fall of objects on Earth to a value of the lunar distance which would accord therewith.1 This Note aims to assess that claim, and will do so in the light of the 100 per cent error in the Principia’s estimate of the lunar relative mass, described by the present writer in 1985.2 Arguing from tidal data, Newton concluded that the Moon was 1/39.788 of the Earth’s mass,3 whereas actually it is a mere 1/81. It will be proposed here that this is the principal source of error in Newton’s Moon-test: it led to a considerable misplacement of the position of the baricentre, which in turn produced an undue contraction of the lunar orbit radius.
The 100 per cent error in Newton’s lunar mass estimate has further implications for the Principia’s Book III, a considerable portion of which consists of lunar theory, and this merits further study: arguably, it is the most significant error in the Principia’s Book III. All that here concerns us is how it led Newton to locate the baricentre outside the Earth, as a point around which the Earth revolved once a month, whereas in fact the baricentre always remains a thousand miles or so below Earth’s surface.
This positioning of the baricentre, which first appeared in the second edition of the Principia of 1712, seems to be the first quantitative computation thereof. The notion of a baricentre had been earlier used by Wren, Hooke and Wallis in their studies of momentum conservation in the 1670s.4 We find no computations of the position of a common centre of gravity in, for example, David Gregory’s Astronomiae ... elementa of 1702, nor in William Whiston’s Lectures in Astronomy of 1710. If we are correct in viewing the 1712 Moon-test as containing the first baricentre computation, then this is a further reason for examining it.
As a result of misplacing the baricentre position, the later version of the Moon-test was notably less accurate than the first one - despite the nine-figure accuracy of its computation. A simple lunar distance of 60 Earth-radii was used in the first edition of the Principia of 1687, for the brief computation of Proposition IV, Theorem IV. The later version of the Moon-test (Proposition XXXVII, Corollary V) appears as a part of a greatly expanded lunar section in the second edition, and adopted a larger value for mean lunar distance of 60.4 Earth-radii, the true figure being 60.27. We now trace the stages of the initial computation as given in the first edition.
The first Moon-test
An accurate estimate of the Earth’s diameter had been published in 1684 in the posthumous works of Jean Picard, giving 692 miles to a degree longitude at the equator .5 It was presumably from this datum that Newton obtained his figure for the circumference of the Earth as 123249600 Paris feet, equivalent to 7936 miles diameter (1 Paris foot = 1.068 imperial feet), a value accurate to within 0.3 per cent. This figure did not change through the different versions of the computation.
We may follow Professor Whiteside’s suggestion as to the likely first steps of the computation:6 multiplying the Earth’s circumference by 60 gave the lunar orbit radius, and dividing the result by the accurately known lunar sidereal month period of 27.32 days gave Newton the Moon’s average speed in its orbit around Earth. Such a computation would have given 38.02 miles per minute - though the figure is not given in the Principia. After this calculation there comes the remarkable conception of how far the Moon would fall towards Earth in one minute ‘if stopped’ in its orbit.
The text here refers to a ‘calculus’ given in Book I, Proposition IV, Corollary IX:7,8 the Moon at A would fall to C ‘if stopped’, AD being the diameter, otherwise the Moon at A would normally move to B in unit time (Figure 1, below) ; then, AB2 = AC x AD.
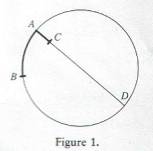
Figure 1: Fall of the Moon ‘if stopped’
The reader will readily derive this Huygens-type formula from first principles. Using the 38.02 miles per minute figure which Newton would have thus derived, the formula yields 15.009 Paris feet in one minute as the free-fall distance AC, not far from the 15 1/12 feet/minute value arrived at in Proposition IV.
From the inverse-square law it would follow that an object on Earth must therefore fall 602 x 15 1/12 feet in one minute. Then, using Galileo’s principle that the distance a body falls is as the square of time, it follows that in one second the object would fall only 15.08 Paris feet - the observed value. (The modern value for comparison is 15.07 Paris feet.)
The computation ignored all the lunar inequalities and treated its path as simple uniform circular motion. The limiting accuracy of such an approach may be found by performing the same computation with modern figures (6.36 x 106 metres for the Earth’s mean radius and 27.32 days for the lunar sidereal period) which gives 9.87 m/s2 for ‘g’. A correction factor for the spin of the Earth at the latitude of Britain needs to be subtracted, equivalent to 0.02 m/s2, after which it can be seen that Newton’s original Moon-test in the first edition of the Principia should give a value of ‘g’ in excess by a mere 0.4 per cent.
No ‘g’ computation
It is worth noting that no explicit conception of acceleration appears in the Moon-test, either verbally or in computation, despite the many accounts which have affirmed this. It has seemed convenient for historians to view the Moon-test computation in terms of the concept of acceleration, and of ‘g’ in particular. To cite just one example, a recent account has described how:
‘Newton calculated the acceleration towards the Earth which the ‘lunar apple’ would experience if it was very near to the Earth’s surface. This turned out to be exactly the same as the acceleration of ordinary falling bodies near the Earth’s surface.’9
Even Westfall refers to the Moon-test as ‘Newton’s “g” computation’10,11 No ‘g’ computation is present anywhere in the Principia, at least in this writer’s opinion. A comparison may be made with the persistent tendency to view the Principia’s Second Law of motion as if it contained a statement about rate of change of momentum, as that is how it later came to be formulated.12,13 Likewise, historians have preferred to treat the Moon-test as though it had been formulated in terms of the acceleration due to gravity, rather than deal with the now arcane geometrical methods used to deal with the motion of falling objects, before algebraic methods of treatment had been devised.
Here we approach the deep issue of the extent to which the Principia’s author was in possession of the methods of differential calculus when composing his master-work. Perhaps it will suffice to quote Bernard Cohen, in his Introduction to the variorum edition of the Principia, concerning the Second Law of motion, that Newton ‘did not ever write... a fluxional equation such as F = kms’’ = kmv’14 (Newtonian notation: two dots over ‘s’ indicate second differential of distance, single dot over ‘v’ indicates rate of change of velocity). Propositions XXXII-XXXIX of the Principia’s Book I (third edition) deal with the acceleration of falling bodies, but do so in a geometrical manner, and without assigning a numerical value to acceleration.
The baricentre position
The later version of the Moon-test appeared in the second edition of 1712 as a corollary to Proposition XXXVII, where an erroneously high value of lunar density has been inferred from tidal data in the Bristol Channel. The computation began with a mean lunar distance from the Earth’s centre of 1187379440 Paris feet, equivalent to the value of 60.4 Earth-radii. The exaggerated baricentre correction was then applied, multiplying by the ratio 39.78/40.78, to give a lunar orbit radius of 1158268534 Paris feet, equivalent to 58.9 Earth-radii. The method thus applied used a principle derived from Book I: ‘For the distances of the bodies from the common centre of gravity are inversely as their bodies’ (Section XI, Proposition XVII). A hefty error had thereby been incorporated into the data, which required some ‘fudge factors’ to iron out.15
By a similar computation to the previous Moon-test, a value of 14.7706353 feet in one minute now emerges, as the distance which the Moon would fall Earthwards ‘if stopped’. This is 2 per cent lower than the value given on earlier pages in Proposition IV, with scant explanation given for the divergence. The discrepancy arose from the smaller lunar orbit radius used. An adjustment factor of 178/177 was then applied, mysteriously expressing the component of solar gravity for which a correction was necessary, to give 14.853 8067 feet in one minute. Lastly, to find the distance which an object on Earth would fall in one second, a scaling adjustment was applied of 60.4 Earth-radii, as before. This factor represents the full lunar distance without any baricentre correction, as was applied earlier in the computation, which is fair enough. Effectively the scaling is done by multiplying by the square of 60/60.4 -but, not precisely: at the start of the argument the maximum diameter of the Earth was taken, at the equator, to derive the lunar radius, while at this later stage returning to Earth so to speak the mean diameter of the Earth is taken. By such a further, somewhat questionable, adjustment factor the damaging effect of the baricentre error is lessened, and this assists in reaching the very close tie-up with observed values at the end. His final figure of 15.11175 feet in one second, or 15’, 1” and 4 1/11 lines (a line being 1/12 of an inch), differs, the text concedes, by a mere 2/3 of a line from the empirically determined value from a Paris pendulum. As Westfall notes, an accuracy of one part in four thousand has been claimed.16
As the only computation to appear twice in the Principia, using two different sets of numerical values, the transition it displays from a one-body to a two-body computation remains of theoretical interest. In passing we may note that the Newtonian ultra-dense Moon seems to have gained acceptance by Newton’s contemporaries William Whiston in his ‘Astronomical Lectures’ of 1710 gave the lunar relative density as 7.00 and Earth’s as 3.87 compared to the Sun as 1.0017 - a relative lunar density even higher than that given in the Principia. Actually the Moon’s mean density is 0.6 that of Earth’s.
We may describe the computations using the customary ‘Newtonian’ equations as follows: if R is the lunar orbit radius around the baricentre, R’ is the Earth-Moon distance, r is the Earth’s mean radius and V is the Moon’s mean speed in its sidereal orbit of period T, then V = 21tR/T, and the Moon’s acceleration towards the Earth = V2/R = gr2/R’2; from which, for an object on Earth, the distance fallen in one second is
½ g = 2π2R/T2(R’ /r)2,
which was in essence the two-body computation performed, where the ratio R’/R is equal to (mass of Earth + Moon)/(mass of Earth). Putting R’ = R gives the computation in modern terms that was performed for the first edition:18
g = 4π2 R3/r2 T2.
Summarizing, it is evident that Westfall’s claim made in his celebrated but still shocking ‘Newton and the fudge factor’ was substantially correct, that the accuracy of the computation has been much exaggerated. The dominant source of error was a 100 per cent overestimation of the Moon’s mass by Newton, whereby an error of just over 1 per cent was introduced into the Moon-test computation of 1712 by the inaccurately placed baricentre. This appears to be the first computation of a baricentre position. Our respect for the achievement involved in this computation is not lessened by appreciating that the tools of calculus were for whatever reason not employed by its illustrious author.
References.
1 R. S. Westfall, ‘Newton and the fudge factor’, Science, (1973), 179, pp. 751-8.
2 N. Kollerstrom, ‘Newton’s lunar mass error’,
Journal of the British Astronomical Association, (1985), 95, pp. 151-3.
3 Philosophiae naturalis principia mathematica, 3rd edn, Book III, Proposition XXXVII, Corollary IV. See also Newton’s System of the World where the mean lunar density is given as 1.5 times that of the Earth (Principia, Motte translation, UCLA Press, 1963 edn, p. 595).
4 J. A. Bennett, ‘Hooke and Wren and the system of the world: some points towards an historical account’, BJHS, (1975), 8, pp. 44-9.
5 J. Picard, Traite du nivellement ... avec une re
lation du quelques nivellements faits par ordre du roy et un abrdge de la mesure de la terre, Paris, 1684.
6 D. T. Whiteside, The Preliminary Manuscripts for Isaac Newton’s 1687 Principia, Cambridge, 1989, p. xi.
7 Corollary IX of Proposition IV of Book I of the Principia: ‘The arc which a body, uniformly revolving in a circle with a given centripetal force, describes in any time, is a mean proportion between the diameter of the circle, and the space which the same body falling by the same force would describe in the same time’ (Motte’s translation, Cajori edition, I, p. 46).
8 H. P. Brougham and E. J. Routh, Analytical View of Sir Isaac Newton’s Principia, 1855, p. 40.
9 J. Roche, ‘Newton’s Principia’, in Let Newton be! (ed. J. Fauvel et al.), Oxford, 1988, p. 56.
10 Westfall, op. cit. (1), p. 752.
11 R. S. Westfall, Never at Rest, Cambridge, 1980, p. 151.
12 C. Truesdall, ‘ A programme towards rediscovering the rational mechanics of the Age of Reason’, Archives for History of Exact Sciences, (1960), 1, p. 23.
13 I. Bernard Cohen, ‘Newton’s Second Law and the concept of force in the Principia’, Texas Quarterly Journal, (1967), 10, p. 128.
14 I. Bernard Cohen, Introduction to Newton’s Principia, Cambridge Mass., 1971, p. 66.
15 Westfall, op. cit. (1), pp. 751-8.
16 Westfall, op. cit. (1), p. 735.
17 W. Whiston, Astronomical Lectures, 1710, Frontispiece.
18 M. Nelkon and P. Parker, Advanced-Level Physics, London, 1981, p. 44.
N. Kollerstrom UCL, STS Dept.