 Step Four
Step Four Department
of
Department
of
Nicholas Kollerstrom's
Newton's 1702 Lunar Theory
|
|
where e is solar eccentricity, 0.01692, H is aphelion, and S is Sun.
For the Moon,
where M is mean lunar longitude.
What is called the solar anomaly (H-S) begins in January as the Sun meets the aphelion line (i.e., where Earth comes nearest to the Sun each year.) This defines a yearly cycle. The Equation of Centre is here required as the orbit is elliptical: two term's have been used for the Sun's Equation, while one will suffice for the Moon as the amplitude of this term is much smaller - 11 arcminutes rather than 2 degrees. [back to flow chart]
where A is the mean apse longitude.
This function goes through one cycle as the Sun moves 180° against the apse line --i.e., its period is six and a half months. It has however a slight amplitude-modulating factor added onto it of a yearly period. Its amplitude varies reciprocally as the cube of the distance, Earth-Sun --that is a bare hint of gravity theory, the nearest TMM gets to such. [back to flow chart]
Mysteriously, this small equation depends upon the Sun-node angle, again having a half-yearly period. [back to flow chart]
 Step Four
Step FourHaving obtained the varying eccentricity e, the twice-equated apse and the thrice-equated moon, as well as the first-equated sun and node, one was ready for the big step, the basic 'equation' for the lunar ellipse. This involved solving the so-called 'Kepler equation' which was quite a headache. The first two terms of the modern equation of centre suffice for this:
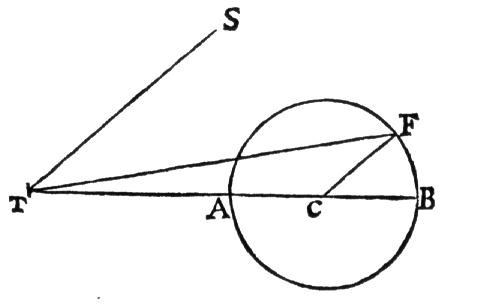
In Figure 1, the mean eccentricity of the lunar orbit is given by a length, TC. (C is the centre of the ellipse while T is the focus where Earth is located.) In modern terms, the centre-focus distance is expressed as ae where a is radius of the circumscribing circle and e is eccentricity.
The varying or equated eccentricity is given by the length TF. In Newton's theory, this varied by ±21% of the mean. Its maximal and minimal values are reached when the sun meets the apse line. So, F is the actual centre of the lunar ellipse in Newton's theory. [back to flow chart]

The above excerpt from Newton's calculations shows him calculating terms such as 'the equation of apogee in ye octant,' 'argumentum annum' (the Sun-apse angle) and 'nodus superior' (the ascending node), for February 22nd, March 7th and April 9th of 1690.
The Variation has a half-lunar period, fortnightly, so that it peaks in the octants (i.e., the 45° positions). Newton has given it an amplitude-modulating factor of yearly period, maximal at perihelion ie in January. This is the largest-amplitude, of over half a degree, except for the Equation of Centre. [back to flow chart]
Step Six
This looks rather obscure, as William Whiston complained in his Lucasian lectures on the subject, and one would not like to specify its period. His comment upon the sixth, made in his Lucasian lectures to students of Cambridge University in 1703, is often quoted:
'How it should come to pass that this sixth Equation of the Moon should arise from Causes which are so unlike join'd together amongst themselves, as are the motion of the Moon from the Sun, and the Motion of the Apogee of the Moon from the Apogee of the Sun; I must acknowledge myself altogether ignorant; nor is there Opportunity for enquiring in these Matters merely Astronomical. In the mean while, I suspect that this Equation was rather deduced from Mr Flamsteed's observations, than from Sir Isaac Newton's own Argumentation.' (Cohen,1975, p.361)
However, modern lunar-equation terms are a lot more complicated than this.
This smallest of Newtonian equations has a monthly period, and its two-arcminute amplitude is modulated by a slow, nine-year cycle, of the apse line rotation.
This is the Reduction, to convert into the plane of the ecliptic, from that of the lunar orbit. It appears as modulated by the sun-node angle.
These yearly equations were invented by Newton. N is position of lunar north node. [back to flow chart]
This derived from Kepler, having a maximum amplitude 1°30' and zero value per sun-node conjunction--i.e., a six-monthly period. [back to flow chart]
A yearly equation, where A is position of mean lunar apogee. [back to flow chart]
In Newton's diagram of the Horrocks epicycle (Figure 1), the second apse equation is the angle FTB. It has up to twelve degrees amplitude and is zero each time the Sun meets the mean apse line (TB in the diagram). As the angle FCB is given as twice the Sun-apse angle, one solves the triangle FTC by the cosine formula.
NB, the lunar perigee really does rock back and forth by a lot more than twelve degrees to this period (twice per 13 months) so this Horrocksian equation is describing a real effect. [back to flow chart]
In Figure 1, the mean eccentricity of the lunar orbit is given by a length, TC. c is the centre of the ellipse while T is the focus where Earth is located. (In modern terms, the centre-focus distance is expressed as ae where a is radius of the circumscribing circle and e is eccentricity).
The varying or equated eccentricity is given by the length TF. In Newton's theory, this varied by ±21% of the mean. Its maximal and minimal values are reached when the sun meets the apse line. So, F is the actual centre of the lunar ellipse in Newton's theory. [back to flow chart]
The contents of this page remain
the copyrighted, intellectual property of Nicholas Kollerstrom. Details.
rev: May 1998 ![]()
![]()