 Department
of
Department
of
Science & Technology Studies
University College London
Nicholas Kollerstrom's
Newton's 1702 Lunar Theory
Introduction
When in 1694 Isaac Newton and David Gregory paid a visit
to the Reverend John Flamsteed, in his newly-established Royal Observatory
at Greenwich, he was there shown a table of lunar longitude observations,
plus a column of associated error values, which Flamsteed had derived from
a lunar theory. These error-values became the stimulus for Newton's great
endeavour to resolve the erratic motions of the Moon. The prediction of
longitude at sea was the most pressing scientific problem of the age, and
the finding of lunar longitude seemed to be a promising approach.
The lunar method used and published by Flamsteed consisted
of three steps or 'equations' and was derived from Jeremiah Horrox. As
the Astronomer Royal, Flamsteed had lost hope of being able to find longitude
by using this approach, though it was the primary reason for the setting
up of the Observatory at Greenwich in 1676, and he viewed use of the positions
of the moons of Jupiter as a more reliable method.
Astronomers started from tables of 'mean motions' which
were points on the ecliptic moving with uniform angular speed, and then
used 'equations' to derive the actual positions of the heavenly bodies
as deviations from these mean motions. First came the 'annual equations'
which in Newton's theory were applied to the node and apse line, as well
as the Sun and Moon. These were called annual because they increased and
decreased in a yearly cycle.
 Horrox's
theory worked kinematically, having a deferent-wheel that revolved once
per conjunction of the Sun and the mean apse line (Figure
1 left). Varying eccentricity and an oscillating apse line were both
linked to the Sun-apse angle. Newton observed to Flamsteed that the Horroxian
theory generated lunar longitude errors of up to twelve arcminutes, which
was far from adequate. For comparison, the prizes offered in the next century
for 'finding the longitude' began at one degree of terrestrial longitude,
which is equivalent to some two minutes of lunar longitude.
Horrox's
theory worked kinematically, having a deferent-wheel that revolved once
per conjunction of the Sun and the mean apse line (Figure
1 left). Varying eccentricity and an oscillating apse line were both
linked to the Sun-apse angle. Newton observed to Flamsteed that the Horroxian
theory generated lunar longitude errors of up to twelve arcminutes, which
was far from adequate. For comparison, the prizes offered in the next century
for 'finding the longitude' began at one degree of terrestrial longitude,
which is equivalent to some two minutes of lunar longitude.
A lunar theory started with
five mean motions, for the Sun, Moon, lunar node, lunar apse and aphelion,
as linearly time-dependent functions moving around the ecliptic. These
then became 'equated' in a series of steps. An 'equation' did not then
signify a formula, but rather a quantity, measured in minutes or degrees,
whereby a mean value was improved, to obtain something nearer to its actual
value. For the lunar nodes, Kepler and Brahe had found just one such equation.
The Sun likewise was given one 'equation' by astronomers, viz its equation
of centre.
In the case of the Moon, from Ptolemy to Copernicus there
had remained two such 'equations', namely the evection and equation of
centre; two more having been added by Kepler and Tycho Brahe, viz. the
annual equation and Variation. The key feature of Horrox's theory was its
compression of the two classical inequalities into one, which caused both
the eccentricity and apse line to co-vary, resulting in a three-stage process:
firstly the annual equation, then the equation of centre, and thirdly the
Variation.

 On
Flamsteed's version of the Horroxian theory,
the annual equation of the Moon had a maximal value of twelve arcminutes,
for the equation of centre this was 6°20',
and for the variation, thirty-eight arcminutes. Thus
the second was far the largest 'equation'. Finally, from the node's equated
position one obtained the 'reduction', to convert longitude positions from
the plane of the lunar orbit to that of the ecliptic.
On
Flamsteed's version of the Horroxian theory,
the annual equation of the Moon had a maximal value of twelve arcminutes,
for the equation of centre this was 6°20',
and for the variation, thirty-eight arcminutes. Thus
the second was far the largest 'equation'. Finally, from the node's equated
position one obtained the 'reduction', to convert longitude positions from
the plane of the lunar orbit to that of the ecliptic.
Newton tried and failed in 1694/5 to infer the lunar inequalities
from his theory of gravity, whereby his initial optimism gave way to frustration.
The first edition of the Principia (1687) had contained nothing
of assistance to the practical astronomer in this respect. It credibly
linked the two inequalities discovered by Kepler and Brahe, viz. the annual
equation and variation, to the new theory of gravity, and it claimed that
the rocking apse line could be likewise accounted for by that theory, however
it lacked what was most desired, namely a procedure for locating lunar
latitude and longitude. The celebrated 'Moon-test' in the First Edition
which linked celestial and terrestrial physics used only simple uniform
circular motion, with the Earth at the centre.
A myth belonging to the 1690s which has rolled down the
centuries is the notion that Newton abandoned his lunar endeavour because
Flamsteed could not or would not provide him with adequate lunar data.
The truth is rather the contrary, that Newton had been supplied with an
unprecedented amount of positional data from Flamsteed -- nigh on two hundred
lunar positions -- of a higher accuracy than any hitherto obtained. It
was rather the inherent difficulty of the problem that caused this failure,
if such it was.
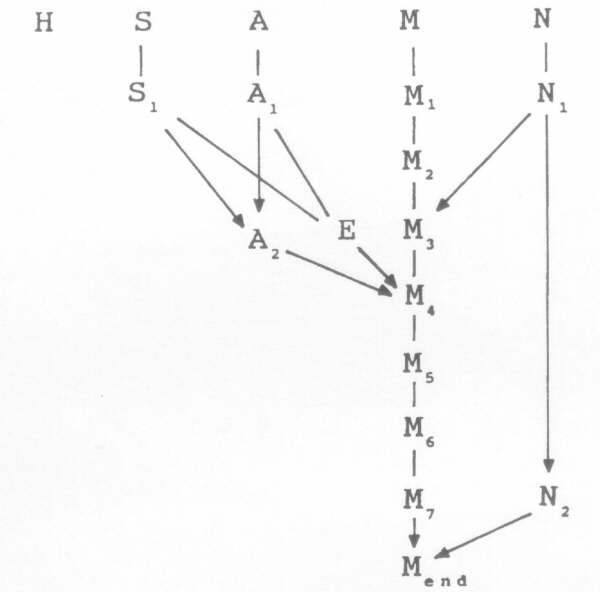
In the year 1702 Newton's 'Theory of the Moon's Motion'
(TMM) was published, in a mathematical-astronomical textbook published
by David Gregory, who gave it its title. (For a facsimile of Gregory's
1715 printing, click here.) It featured
six new 'equations', such that the Moon became equated seven times.
Its procedure is given as a flow diagram in Figure 2 (right), where the
symbols refer to the values in celestial ongitude of:
-
H: aphelion
-
S: Sun
-
A: apse (lunar apogee)
-
M: Moon
-
N: lunar node
For a detailed description of the computational steps, click
here.
The new lunar equations are the second, third, sixth and
seventh, with the annual equation as the first and the Variation as the
fifth. Also the node and apse line were given 'annual equations', making
them vary seasonally. A Horroxian equation of centre forms the central
fourth 'equation' of TMM, using the varying eccentricity E and the twice-equated
apse A2.
A Modern Reconstruction
My PhD thesis used a computer program that modelled Newton's
steps of equation, replicating the steps of Newton's 1702 Theory of Lunar
Motion. Its 'equations' can normally be represented by sine and cosine
functions; for example, the Variation is represented by 35'23"sin2(S1-M4),
an expression which reaches its maxima and minima in the octants. The term
M4 means that the fourth-equated value of lunar longitude is
used. It has been subtracted from the first-equated value of solar longitude,
S1. However, TMM also specified that the maximum amplitude of
the Variation itself varied seasonally, becoming greatest at perihelion.
It was to vary 'reciprocally as the Cube of the Distance of the Sun from
the Earth'. Accordingly, TMM's fifth lunar equation was represented by:
M5 = M4 + 35'23"[1 - 3Ecos(H-S)] [sin2(S1-M4)]
where E is the Earth's eccentricity.
To the mean apse, TMM added first an annual equation,
here modelled by 20'sin(H-S), which maximises at the equinoxes. This gave
A1, the first-equated apse value. The second equation of the
apse was far larger and varied with the Sun's angle against this mean apse,
adding which transformed A1 into A2. We may write:
A2 = A1 + f(S1-A1)
where f is a function using the cosine rule derived from
the Newtonian instructions, as a trigonometric equivalent. Figure
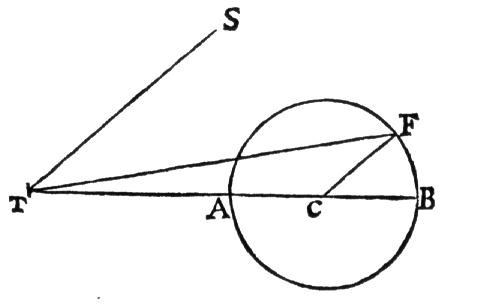
1 shows TMM's diagram of this second apse equation.
An 'equation of centre' signified the divergence from
uniform circular motion due to elliptical motion according to Kepler's
second law. It had zero magnitude at the apogee/perigee positions and for
the lunar orbit reached its maximum value of around seven degrees near
the quadratures. Its solution involved approximations to the 'Kepler equation',
or some other method for those astronomers who had not accepted Kepler's
second law.
In creating the reconstruction of TMM, there was one stage
where a modern formula was used in place of the historic procedure. Gingerich
and Welther at the Smithsonian Institute found that Flamsteed's 'Equation
of Centre' tables as published in 1681 concurred with values derived using
the modern equation of centre formula within several arcseconds (Gingerich
and Welther, 19734). See, Equation of Centre.
Flamsteed was, they concluded, the first to prepare such tables based upon
a solution of Kepler's area law. Newton's TMM of 1702 merely indicated
that tables should be found for 'the Equation of the Moon's Centre, as
in the common way'. Accordingly, the TMM program used the modern equation
of centre, with input as the anomaly (A2-M3) and
the eccentricity E.
|
To download TMM Replica 2.0
"Newton's Theory of the Moon's Motion"
package click here
|
To view a sample
of these calculations by Newton
click here
|
Figure 1: The Horroxian epicycle
in Newton's 1702 lunar theory, where T is Earth, at one focus of the orbit-ellipse,
S that of the Sun, TB the mean apse, C the mean centre of the lunar orbit
and F the 'equated' centre of the lunar orbit. TC represents the mean eccentricity
and TF the varying eccentricity and angle FTC the second apse equation.
The line CF revolves once per sun-apse line conjunction; this implies that
the angle FCB is twice STA, though Newton has not well shown this. STB
was alluded to as the 'annual argument.'.
Figure 2: The steps of equation
given to the five mean motions of aphelion, sun, lunar apse, Moon and lunar
node, as H, S, A, M and N, in Newton's 1702 lunar theory. For the details
of the computational stes, click here.
This introduction is derived from Nicholas Kollerstrom.
1996: "'A Reintroduction of Epicycles': Newton's 1702 Lunar Theory and
Halley's Saros Correction," Quarterly Journal of the Royal Astronomical
Society 36:357-368.
The contents of this page remain
the copyrighted, intellectual property of Nicholas Kollerstrom. Details.
rev: May 1998 

 Horrox's
theory worked kinematically, having a deferent-wheel that revolved once
per conjunction of the Sun and the mean apse line (Figure
1 left). Varying eccentricity and an oscillating apse line were both
linked to the Sun-apse angle. Newton observed to Flamsteed that the Horroxian
theory generated lunar longitude errors of up to twelve arcminutes, which
was far from adequate. For comparison, the prizes offered in the next century
for 'finding the longitude' began at one degree of terrestrial longitude,
which is equivalent to some two minutes of lunar longitude.
Horrox's
theory worked kinematically, having a deferent-wheel that revolved once
per conjunction of the Sun and the mean apse line (Figure
1 left). Varying eccentricity and an oscillating apse line were both
linked to the Sun-apse angle. Newton observed to Flamsteed that the Horroxian
theory generated lunar longitude errors of up to twelve arcminutes, which
was far from adequate. For comparison, the prizes offered in the next century
for 'finding the longitude' began at one degree of terrestrial longitude,
which is equivalent to some two minutes of lunar longitude.
 Department
of
Department
of

 On
On
